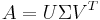Fundamental theorem of linear algebra
In mathematics, the fundamental theorem of linear algebra makes several statements regarding vector spaces. These may be stated concretely in terms of the rank r of an m×n matrix A and its singular value decomposition:
First, each matrix 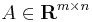 (
( has
has  rows and
rows and  columns) induces four fundamental subspaces. These fundamental subspaces are:
columns) induces four fundamental subspaces. These fundamental subspaces are:
| name of subspace | definition | containing space | dimension | basis |
|---|---|---|---|---|
| column space, range or image | 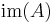 or or 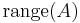 |
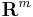 |
 (rank) (rank) |
The first  columns of columns of 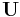 |
| nullspace or kernel | 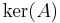 or or 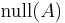 |
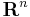 |
 (nullity) (nullity) |
The last 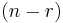 columns of columns of 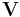 |
| row space or coimage | 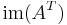 or or 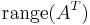 |
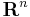 |
 |
The first  rows of rows of 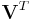 |
| left nullspace or cokernel | 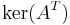 or or 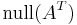 |
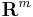 |
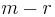 |
The last 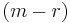 rows of rows of 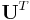 |
Secondly:
- In
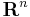 ,
, 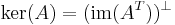 , that is, the nullspace is the orthogonal complement of the row space
, that is, the nullspace is the orthogonal complement of the row space - In
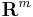 ,
, 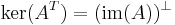 , that is, the left nullspace is the orthogonal complement of the column space.
, that is, the left nullspace is the orthogonal complement of the column space.
The dimensions of the subspaces are related by the rank–nullity theorem, and follow from the above theorem.
Further, all these spaces are intrinsically defined – they do not require a choice of basis – in which case one rewrites this in terms of abstract vector spaces, operators, and the dual spaces as 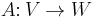 and
and 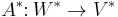 : the kernel and image of
: the kernel and image of 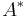 are the cokernel and coimage of
are the cokernel and coimage of  .
.
See also
References
- Strang, Gilbert. Linear Algebra and Its Applications. 3rd ed. Orlando: Saunders, 1988.
- Strang, Gilbert (1993), "The fundamental theorem of linear algebra", American Mathematical Monthly 100 (9): 848–855, doi:10.2307/2324660, JSTOR 2324660, http://www.eng.iastate.edu/~julied/classes/CE570/Notes/strangpaper.pdf
External links
- Gilbert Strang, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWare
|
|||||||||||